What Is Dimensional Formula?

Dimensional formula and dimensional equations of a physical quantity are defined as the fundamental quantities that are raised to powers to express the physical quantity. The basic dimensional formula of mass is [M], the length is [L] and time is [T].

The other way of defining dimensional formula is, the physical quantities are expressed in terms of their basic units. For example, the dimensional formula of force is given as:

F = [MLT^-2]

The unit of force is Newton or kg.m.s^-2.

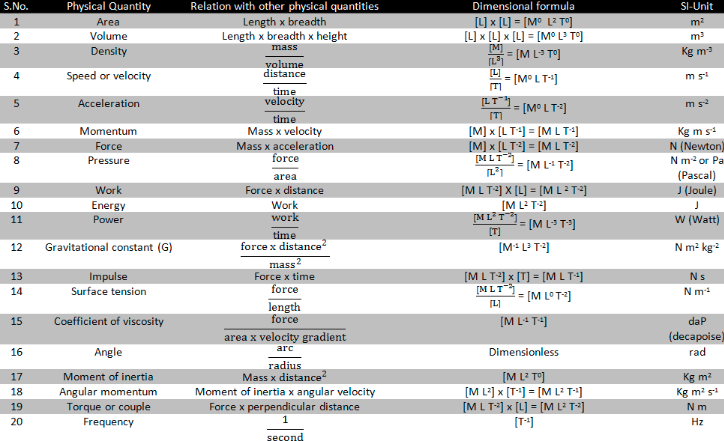
For any physical quantity, the dimensional formula is written when its relation with other physical quantities is known. Following is a table of the dimensional formula of a few quantities.

Physical quantity	Relation with other physical quantities	Dimensional formula	SI unit
Area	Length * Breadth	[L]*[L] = [M0L2T0]	m2
Volume	Length * Breadth * Height	[L]*[L]*[L] = [M0L3T0]	m3
Density	(Mass)/(Volume)	[M]/[L3] = [ML-3T0]	kg.m-3
Energy	Work	[ML2T-2]	J
Impulse	Force * Time	[MLT-2]*[T] = [MLT-1]	N.s

What is dimensional equation?

The dimensional equation is defined as the equation with dimensional formula. By equating the dimensional formula on the right-hand side and on the left-hand side, the dimensional equation is obtained. This is proved with the help of the principle of homogeneity.

What is the principle of homogeneity?

The principle states that the dimensions on the left-hand side of an equation must be equal to the dimensions on the right-hand side. Using the principle of homogeneity one can even convert the units from one system to another. Example of the principle of homogeneity is as follows.

Dimensional equation of v = u + at is:

[M⁰LT^-1] = [M⁰LT^-1] + [M⁰LT^-1] * [M⁰L⁰T] = [M⁰LT^-1].

What are the uses of dimensional equations?

Following is a list of uses of dimensional equations.

●     It is used to check the correctness of the physical quantity.

●     It can be used to derive the relation between different physical quantities.

●     The dimensions of constants can be found using the dimensional equation.

What are the limitations of dimensional analysis?

Following are the limitations of dimensional analysis.

●     There is no information about the quantity being scalar or vector quantity.

●     The formula cannot be derived if the quantity depends on more than three factors.

●     Dimensional analysis cannot be carried for functions like logarithmic functions, exponential functions, and trigonometric functions.

Interested to learn more about dimensional analysis and other Physics related concepts like wavemotion, types of dc motors, etc, visit BYJU’S.